Introduction

The proliferation of quantitative analysis and algorithmic investment have forced data scientists to direct their mindshare towards solving a new challenge. 

There are simply too many good and predictive data sources!

New innovative and informative data is entering the market daily, all aggressively pursuing a finite group of asset managers who are looking to gain a competitive edge. However, not all datasets can be used together. In addition to likely “overfitting galore”, a model with too many factors will have a difficult time generalizing an outcome that is both predictive, defensible, and interpretable for comfortable consumption by asset managers. 

It is therefore incumbent upon the data scientist and quants to inform their financial models which subset of features ought to be used together. This decision depends on market conditions, the given constituent universe, and the defined outcome objectives.

Effectively applying machine learning to financial markets requires reducing noise to the greatest extent possible. One approach for doing so is feature selection – the process of choosing an “ideal” subset of features with which to train a model. Parsing away all but the most useful features removes noise from the dataset, thereby ameliorating the learning process.

Why is Feature Selection Difficult?

Quantifying when a feature is “good” or “bad” is a tricky task. In order to remove human discretion from the feature selection process, scientists often resort to two general approaches:

• The Threshold Approach
• The Select-K-Best Approach

Assume some feature assessment algorithm assigns each feature an importance score, which is nothing more than a floating point value between 0 and 1 (scaled from 0 as worst to 1 as perfect score). Using the threshold approach, all features below a predefined threshold are parsed from the training set. This method is useful in that it guarantees a minimum importance for the remaining features. The drawback is that it is often difficult to intuit what constitutes an appropriate threshold – low thresholds can be subject to false positives due to noise, whereas high thresholds can be overly punitive and remove useful information.

In the second approach, using select-k-best, the k features with highest importance are maintained while the rest are removed. This method is useful in that it ensures that our model will have a minimum amount of “best” data on which to train, from what is available. The drawback is that simply choosing the k best makes no guarantees regarding the quality of the underlying data. This approach is therefore also subject to false positives due to noise.

A side note: There are other viable approaches to feature selection, one of which utilizes genetic algorithms (GA). We have written of this technique previously, and it is certainly a viable alternative – see link here.

Introduction to Permutation Importance

Permutation importance is a feature selection technique that helps solve the aforementioned problems. This process works as follows:

• Divide a dataset into a training and validation set
• Train your model on the training set and calculate performance metric on the validation set
• For each feature:

shuffle the chosen feature in the validation set, then calculate performance metric on validation set.

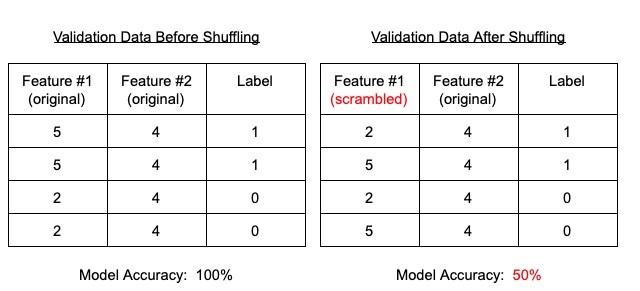
Figure 1: Example of the permutation importance process applied to Feature #1

The leftmost table of Figure 1 shows an “initial” validation set. Note that Feature #1 is strongly predictive: a value of 5 indicates a positive class label and a value of 2 indicates a negative class label. Feature #2, on the other hand, has no predictive value whatsoever. With this data (Feature #1 in particular) our model is able to achieve 100% accuracy on the validation set.

Using permutation importance, Feature #1 is randomly shuffled. Now, as shown in the rightmost table of Figure 1, the relationship between the value of Feature #1 and the class label has been broken; Feature #1 is no longer predictive. For this reason, our model accuracy on the shuffled validation set plummets to 50%.

What did this process teach us about the data? We learned that Feature #1 is important because destroying its underlying signal (via random shuffling) removes the model’s ability to make good predictions. Specifically, the importance of Feature #1 is numerically expressible as 100% – 50% or 1.0 – 0.5 = 0.5. Using permutation importance the utility of a feature is measured as the decrease in model performance caused by corrupting said feature via shuffling.

Permutation importance repeats this process to calculate the utility of each feature. Any variance caused by the random shuffling is easily dampened by simply running multiple iterations of permutation importance and averaging the results.

Improving Permutation Importance

Recall that a weakness of both the threshold and select-k-best paradigms was an inability to ascertain the correct parameters (threshold or k value) to minimize false positives due to noise. Permutation importance quantifies the significance of each feature and therefore can determine an importance value attributable to random noise. This is done by simply adding a “random noise” feature to a dataset prior to running permutation importance. The importance value of “random noise” can then be used as a threshold heuristic to immediately eliminate equal or worse performing features from the dataset. Now, when threshold or select-k-best is applied, the resulting feature subset is guaranteed theoretically to be more predictive than random data.

Additional Benefits of Permutation Importance

Permutation importance has several additional properties that make it attractive for feature selection. First, it is model agnostic making it a viable choice for any machine learning pipeline. Secondly, permutation importance makes no assumptions about the data, instead it computes feature values empirically. As a result, permutation importance is able to account for the fact that features not valuable to one model could provide a great deal of benefit for a different model. Furthermore, because importances are calculated on out of sample data, the score values indicate feature significance for generalizing the model to new data.

Drawbacks of Permutation Importance

Although permutation importance is an excellent tool, it does have its drawbacks. Most obviously, multiple iterations of permutation importance has the potential to increase runtime. In many machine learning contexts calling a model’s predict() function is a relatively fast operation, but for more complicated systems the increase in computational overhead is worth considering.

A second potential hurtle is the fact that permutation importance can be “fooled” when features are correlated. Consider two features, A and B, that are very predictive and strongly correlated. Shuffling feature A likely produces only a small decrease in performance as very similar information is present in feature B. For this reason, permutation importance tends to be overly punitive and assigns low importance values to correlated features. For this reason, preprocessing by removing correlated features is necessary prior to running permutation importance. 

Conclusion

Building great machine learning models necessitates getting the most out of all available datasets. Because available data is growing exponentially, we strive to reduce dimensionality through feature selection. Feature selection via permutation importance is an excellent technique for removing noisy features. By leveraging a synthetic “random noise” feature, we can form a threshold or select-k-best parsing, so that a dataset’s underlying signal can be magnified. These steps reduce the likelihood of overfitting, while improving and accelerating the learning process.